Simple Pendulum

A simple pendulum is a heavy mass (bob) suspended by very low weight inextensible and flexible string which undergo to and fro motion in a plane from mean position. This to and fro motion of pendulum becomes simple harmonic motion for small angle of oscillation. Let is consider a simple pendulum with mass ‘m’ and length of the string as ‘l’. Let us displace the bob from mean position by small angle $\theta$ . This displacement should be as small as possible. Once this is displaced we release the bob and we can see the oscillation from mean position. Let us breakdown the force acting on this bob

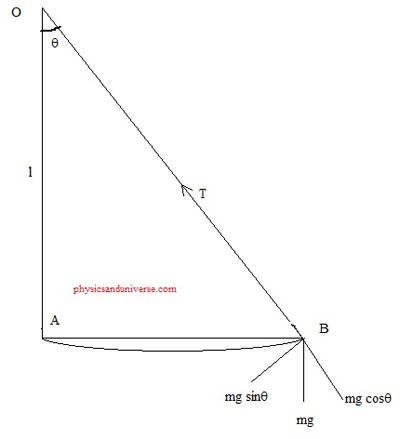
1. mg, the weight of bob acting vertically downward.

2. Tension of the string T with direction towards the point of suspension

3. $mg sin\theta$ acting towards the mean position

4. $mg cos\theta$ acting away from suspension point

When the bob is at rest the component T and $mg cos\theta$ act opposite to each other and these forces balances out each other.

The force $mg sin\theta$ tries to bring the bob towards the mean position and this force is called restoring force. During the process or restoration to mean position, an acceleration ‘a’ is produced towards the mean position so,

$-mgsin\theta = ma$ negative sign indicates that force is opposite to displacement.

$-g sin\theta = a$

$\theta$ is as stated earlier is very small so, in radian system of measurement we can approximate like $sin\theta \equiv \theta$

$a = -g\theta$

We also have

$\theta = \dfrac{Arc}{Radius} = \dfrac{Arc AB}{l}$

If we assume that l is very long and $\theta$ is very small (less than 4 degree) then the arc AB will be almost equal to linear displacement ie AB. So, Arc AB = x

$\theta = \dfrac{x}{l}$

Using this value of $\theta$ in $a = -g\theta$ we get

$a = -g \dfrac{x}{l} = - \dfrac{g}{l} x$

$\dfrac{a}{x} = - \dfrac{g}{l}$ ……………. (1)

The negative sign indicate that the acceleration is towards the mean position. In a pendulum we can assume that length of pendulum ‘l’ is constant and so is ‘g’. Hence we get

$a \propto x$

Now see that the acceleration of bob is proportional to displacement and is directed towards the mean position, we can say the the motion is Simple Harmonic Motion. Therefore we have

$\dfrac{a}{x} = -\omega^2 =-(\dfrac{2\pi}{T})^2$ ………….. (2)