Let P be a particle on a smooth plane inclined at an angle alpha to the horizon. If ABC represent a vertical section of the inclined plane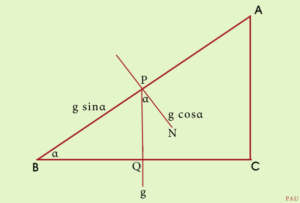 through P, AB is the line of greatest slope and the angle ABC is alpha. The acceleration of P due to gravity is g and it is vertically downwards towards PQ. If PN be normal to the plane then angle QPN is alpha. The resolved parts of g are
through P, AB is the line of greatest slope and the angle ABC is alpha. The acceleration of P due to gravity is g and it is vertically downwards towards PQ. If PN be normal to the plane then angle QPN is alpha. The resolved parts of g are along PN and
along PB.
Since the plane prevents any motion perpendicular to it, the particle moves down the plane along AB with acceleration
If h be the height AC and l the length AB of the inclined plane
Let a particle slide down AB from rest and v be its velocity at B.
Then
Thus the velocity acquired is independent of alpha and is the same as the velocity acquired in falling through a height h.
If t be the time taken to slide down AB,
If the particle is projected upwards along BA, its acceleration is






