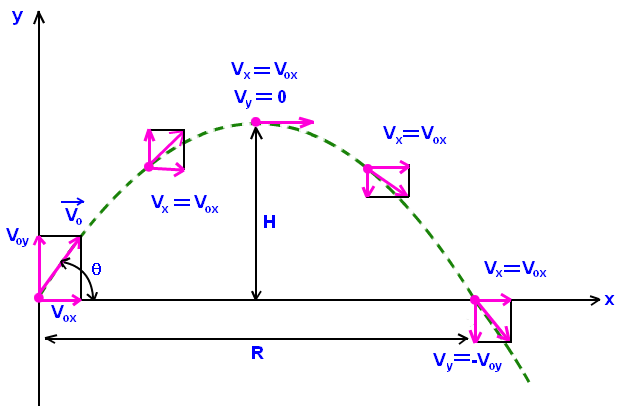
Let us suppose that an object is thrown from a certain height ‘h’ above the ground in horizontal direction with initial velocity ‘u’. This horizontal velocity remains unaffected by the acceleration due to gravity. In this case ‘g’ remains constant throughout the motion. There are two way motion in the projectile, one is vertical motion and another is horizontal motion.

Vertical motion
Just after the projectile is thrown, its initial vertical velocity is zero. The vertical velocity will increase with time and is give by
v=u+gt
u=0
v=gt …. (1)

Now to calculate the time to reach the ground from the height h we have
h=ut + \frac{1}{2}gt^2
h=\frac{1}{2}gt^2
t=\sqrt{\frac{2h}{g}}

Horizontal motion
The time taken by the projectile to reach the ground is calculated above. During this time the projectile moves in the horizontal direction and covers certain distance. This distance is called range. The horizontal range covered is given by the equation
R=ut+\frac{1}{2}at^2
a=0 in horizontal direction
R=ut
Here t is the time projectile stays in the air and is calculated above. Hence using that equation we can calculate range as
R=u\sqrt{\frac{2h}{g}}