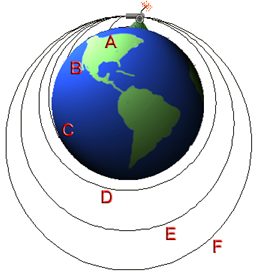
The motion of heavenly objects like Planets, sun, natural satellites etc has drawn a lot of attention in the past the the mystery of their motion remain unsolved until 1665. Sir Issac Newton at the age of 23 made one of the biggest contribution to Physics by simply showing that the force by which moon revolves around the Earth is same force responsible for causing apple to fall to the ground. Sir Issac Newton extended this idea and mad his famous law of Gravitation. The statement of this law states that

Every body in the Universe attract another body with a force called Gravitational force and this force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Let is assume two bodies with masses m_1 and m_2 kept at a distance of r from the centers of the body. If we represent the gravitational force between these two bodies by F then

F \propto m_1m_2 and

F \propto \frac{1}{r^2}

Combining these two relations we get,

F \propto \frac{m_1m_2}{r^2}

or, F = G \frac{m_1m_2}{r^2}

Here G is a constant called Universal gravitational constant and its value is 6.67 \times 10^{-11} Nm^2kg^{-2}

G can also be defined  as – When to object of masses 1 kg each are kept at a distance of 1m then the gravitational force produced between these two objects is 6.67 \times 10^{-11} N

Gravitational Field  Intensity

Gravitational field intensity at any point on the gravitational field is the force exerted by the body on unit mass placed at that point. The value of gravitational field intensity decreases as we move further from the body. The formula for Gravitational field intensity is

Intensity = G \frac{M_E}{R^2}

The unit of Gravitational field intensity is Nkg^{-1}

Acceleration due to Gravity

The gravity of the earth is the force on a body near the surface of the earth and this force is given by

F=G\frac{M_Em}{R_E^2}

Newton’s second law of motion  says the force produced in a body is product of its mass and acceleration

F=ma

Comparing these two equations we get

a=G\frac{M_E}{R_E^2}

This acceleration is represented by g and is called acceleration due to gravity and is given by

g=G\frac{M_E}{R_E^2}

The standard value of acceleration due to gravity ‘g’ on the surface of the earth is 9.81ms^{-2} . This relation shows that the acceleration due to gravity is independent of the mass of the body. This is the reason all body fall to the surface of the earth at the same time irrespective of their masses. Famous feather and coin experiment demonstrates this fact.

Mass of Earth

We now have g=G\frac{M_E}{R_E^2}
After some manipulation we get the mass of earth as
M_E = g\frac{R_E^2}{G}

Density of Earth

To find the density of earth we make some assumptions. We consider earth as homogenous sphere of radius R_E The volume of this sphere is given by
V = \frac{4}{3}\pi R_E^3
Therefore the density of earth is
\rho_E = \frac{M_E}{V}
\rho_E = \frac{3g}{4\pi GR_E}