Circular motion refers to the movement of an object in a circular path. By circular we mean motion about a fixed point. The most suitable examples of circular motion includes motion of the planet around the sun (they are not exactly circular but calculation gets easier and we approximate them to be circular) and stone whirled in circle by attaching it to a string.
Angular Displacement
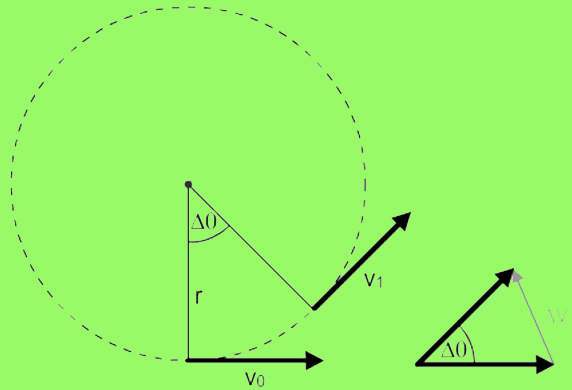
In circular motion, the distance of object from a fixed point remains the same. The angle described at the center of the circle by the an object moving in the circle is called angular displacement. Its unit is radian. It is defined as the ratio of arc length to radius of circle
It is a vector quantity with direction perpendicular to the plane of the circle.
Angular Velocity
It is the angle described at the center in one second by a particle moving in a circle. Mathematically, we can write angular velocity as
Its unit is rad/s. Dividing above equation by we get
where
is linear velocity.
This is also the relation connecting linear velocity and angular velocity of an object moving in a circle of radius r. Angular velocity is a vector quantity with direction perpendicular to the plane of circle.
Frequency and time period in circular motion
Frequency is the number of complete revolutions made in one second by an object moving is a circle. Time period is the time required to make one complete rotation in a circle.
Time period
Angular velocity
Centripetal acceleration and centripetal force
Any object moving is a circular path of radius r and uniform speed v has an acceleration towards the center and this acceleration is given by
To produce this acceleration a force is necessary which is also directed towards the center. This force is centripetal force and is given by
This force is directed towards the center.
Centrifugal force
Centrifugal force is the apparent force that draws a rotating body away from the center of rotation. Centrifugal force is known as an outward force visible in a rotating frame of reference. It is also called a fictitious force in the sense that it is not part of an interaction but is a result of rotation.