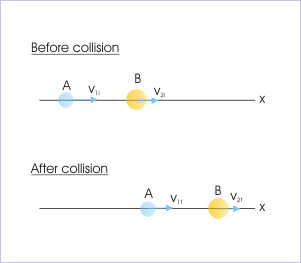
Elastic collision in one dimension

Any collision is elastic if the total kinetic energy of the colliding particles remains conserved. Let us consider two bodies A and B with masses $m_1$ and $m_2$ are moving with the initial velocity $u_1$ and $u_2$ respectively in the same direction and same straight line. In this problem let us suppose that velocity of one object is greater than other $(u_1 > u_2)$ and they are on the collision path. In this situation object A will collide with B and this is called head on collision. After collision and according to our assumption velocity of A will decrease to $v_1$ and velocity of B will increase to $v_2$ If both objects are moving on the same direction after collision then we can say that
Total initial momentum of A and B before collision = $m_1u_1 + m_2u_2$
Total final momentum of A and B after collision = $m_1v_1 + m_2v_2$

According to conservation of momentum principle
$m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2$
$m_1(v_1-u_1) = m_2(u_2-v_2)$ ——- (1)

Total kinetic energy of the particles before collision
$KE_i = \frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2$

Total kinetic energy of the particles after collision
$KE_f = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$

For perfectly elastic collision $KE_i = KE_f$
$KE_i = \frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2$
$m_1(v_1^2-u_1^2) = m_2(u_2^2-v_2^2)$
$m_1(v_1-u_1)(v_1+u_1) = m_2(u_2-v_2)(u_2+v_2)$
Dividing above equation by (1) we get
$(u_1-u_2) = -(v_1 - v_2)$ ——- (2)

Here $(u_1-u_2)$ is the relative velocity of approach of A towards B and $(v_1-v_2)$ is the relative velocity of separation of B and A.

Equation (2) can also be written as
$u_1+v_1 = u_2+v_2$

Let us multiply above equation by $m_2$ and add equation (1) followed by some rearrangement we get
$v_1 = \frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2$

Similarly let us multiply above equation by $m_1$ and subtracting equation (1) followed by some rearrangement we get
$v_2 = \frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2$

Note 1: If mass of A is very very higher than B we can see that the velocity of A remains unchanged while that of body B changes after collision.
Note 2: If object A is much more smaller than B then velocity of A is changed but the velocity of B remains same.
Note 3: If mass of both body A and B are equal then the velocity if the particles are interchanged. $v_1=u_2$ and $v_2=u_1$