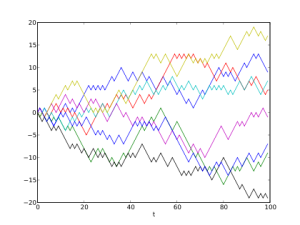
Consider a starting position at some zero point. We toss a coin that tells a man to move forward or backward. He ends up at either the +1 or the -1 position, the next toss of the coin will take him to the +2 or the 0 position, depending on whether the toss tells him to move forward or back. Similarly from the -1 position he could move to zero or -2. An individual photon at the stellar core may be absorbed, re-emitted, absorbed again and re-emitted many times in succession. The direction in which the photon is emitted may bear no relation at all to the direction in which it was traveling just before absorption. The photon may then travel randomly, until it reaches the surface of the star.

Random walk

Random Walk

This random walk can be described statistically. We can estimate the total distance covered by the photon before final escape and at any time in its travel, we can predict the approximate distance of the photon from the star. An individual photon at the stellar core may be absorbed, re-emitted, absorbed again and re-emitted many times in succession. The direction in which photon is emitted may bear no relation at all to the direction in which it was traveling just before absorption. The photon may then travel randomly, until it reaches the surface of the star.

Radiative energy transport can be described as a random walk, where a photon repeatedly absorbed and re-emitted in a random direction. Let the step length of the walk (the mean free path) be d. Consider, for simplicity, the random walk in a plane. After one step the photon is absorbed at

x_1 = dcos\theta_1
y_1 = dsin\theta_1

where \theta_1 is an angle giving the direction of the step. After N steps the coordinates are

x = \sum_{i=1}^{N} dcos\theta_i

y = \sum_{i=1}^{N} dsin\theta_i

and the distance from the starting point is,

r^2 = x^2 + y^2

= d^2 [(\sum_{i=1}^{N} dcos\theta_i)^2 + (\sum_{i=1}^{N} dsin\theta_i)^2]

The first term in square brackets can be written as,

(\sum_{i=1}^{N} dcos\theta_i)^2 = (cos\theta_1 + cos\theta_2 + ..... + cos \theta_N)^2

= \sum_{i}^{N} cos^2 \theta_i + \sum_{i \neq j}{} cos\theta_i cos\theta_j

Since the directions \theta_i are randomly distributed and independent,

\sum_{i \neq j}{} cos\theta_i cos\theta_j = 0

The same result applies for the second term in square brackets. Then,

r^2 = d^2 \sum_{1}^{N} (cos^2 \theta_i + sin^2 \theta_i)

= Nd^2

r = d\sqrt{N}

After N steps the photon is at the distance r = d\sqrt{N} from the starting point. Given a mean free path of photon d and a random distribution of scattering angles, determine overall displacement r after a certain number N scattering events.

Thus, the statistical average of the overall displacement r after N steps is simply d\sqrt{N} .

The time taken by photon to reach the surface from the center depends on the mean free path that is d.

We know that

d = \frac{1}{k\rho}

Here, k is the mass absorption coefficient and \rho is the density (that is mean density of the radiative core). For a typical 1 solar mass star,

k = 10 m^2/Kg

\rho = 2000 kgm^{-3}

Thus,

d = \frac{1}{k\rho} = 10^{-4} m

Now, the number of steps needed to reach radius r,

N = (\frac{r}{d})^2

We know that the solar radius r \sim 10^{9} m

Thus the number of steps is

N = (\frac{10^9}{10^{-4}})^2 = 10^{26}

The total path traveled by the photon is

S = Nd = 10^{26} \ast 10^{-4} m

S = 10^{22} m

and the time taken is

t = \frac{S}{c} = \frac{10^{22}}{10^8} = 10^{14} sec

\approx 10^7 years

This is a very rough and highly approximated calculation and gives a time of 10^7 years as the time taken by the photon to reach the surface of the Sun.