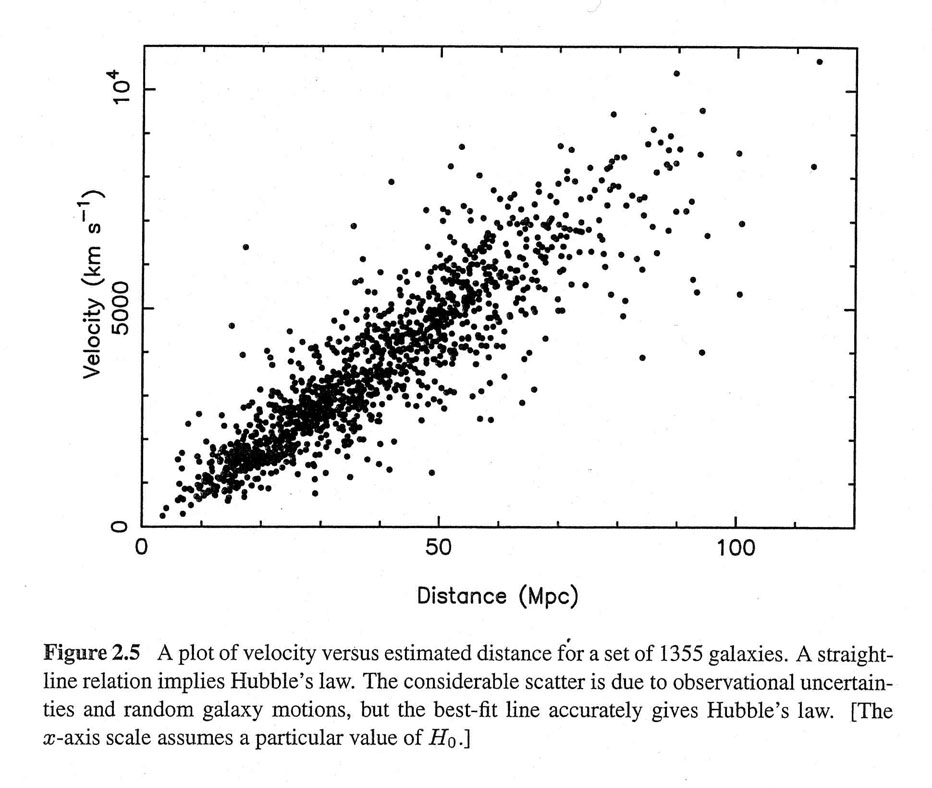
E. Hubble determined that there is a relation between the distance of various galaxies and their radial velocity. The radial velocity was derived from the Doppler shift of absorption lines in the spectrum of the galaxy. The observation of Cepheid variable stars in spiral nebulae enable Hubble to calculate the distance to these objects. Hubble noticed that the amount of redshift in the absorption is proportional to the distance of the galaxy, \upsilon = H_{0}d where \upsilon is the recession velocity, typically expressed in km/s. H_{0} is the Hubble constant and corresponds to the value of H (termed as Hubble parameter which is time dependent and can be expressed in terms of the scale factor) in the Friedmann equation. This value is the same throughout the universe for a given co-moving time. Here ‘d’ is the proper distance from the galaxy to the observer, measured in Mpc. Current best estimates for H_{0} is 73 km/s/Mpc.

Since the Hubble constant is only a constant in space, not in time, the radius of the Hubble sphere may increase or decrease over various time intervals. The subscript ‘0’ in Hubble constant indicates the value of the Hubble constant today. Current evidence suggests that the expansion of the universe is accelerating. This means that for a given galaxy, the recession velocity \frac{dD}{dt} is increasing over time as the galaxy moves to greater and greater distances. However Hubble parameter is actually thought to be decreasing with time. This means that if we were to look at some fixed distance D and watch a series of different galaxies pass that distance, later galaxies would pass that distance at a smaller velocity than earlier ones.

The redshift is usually described as a ‘redshift velocity’, which is the recessional velocity that would produce the same redshift if it were caused by a linear Doppler effect.

\upsilon_{rs} = cZ

here, Z = \frac{\lambda_0}{\lambda_e} - 1 = \sqrt{\frac{1+\upsilon/c}{1 - \upsilon/c}}-1

here, \lambda_0 and \lambda_e are the observed and emitted wavelengths. The redshift velocity \upsilon_{rs} is not so simply related to real velocity at larger velocities.

The value of Hubble parameter changes over time either increasing or decreasing depending on the sign of the declaration parameter q which is defined by,

q = -(1+\frac{\dot{H}}{H^2})

Here, q determine the nature of the space that is overall geometry of the universe. In a universe with a declaration parameter equal to zero (flat curvature), it follows that

0 = -(1+\frac{\dot{H}}{H^2})

H^2 = \frac{dH}{dt}

H^2 dt = dH

H^2 t = H by integration

So, we get H = \frac{1}{t}

or, t=\frac{1}{H}

the time t is the time since the Big Bang. A non zero, time dependent value of q simply requires integration of the Friedmann equations backwards from the present time when the co-moving horizon size was zero.

Thus, the age and ultimate fate of the universe can be determined by measuring the Hubble constant today and extrapolating with the observed value of the declaration parameter characterized by values of density parameters ( \Omega_M for matter and \Omega_{\Lambda} for dark energy).

It was long thought that q was positive indicating that the expansion is slowing down due to gravitational attraction. This would imply an age of the universe less than \frac{1}{H} (which is about 14 billion years). For instance, a value of q is \frac{1}{2} (once favored by theorists) would give the age of the universe as \frac{2}{3H} . In the year 1998, it was discovered that q is apparently negative, meaning that the universe could actually be older than \frac{1}{H} . However the estimate regarding the age of the universe are very close to \frac{1}{H} .