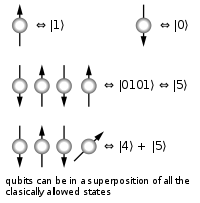
A classical computer performs operations using classical bits which can be either 0 or 1. Now in contrast a quantum computer uses quantum bits or qubits and they can be both 0 & 1 at the same time and it is this that gives a quantum computer its superior computing power. There are a number of physical objects that can be used as a qubit, a single photon a nucleus or an electron. Researchers are using the outermost electron in phosphorus as a qubit.
How it works?
well all electrons have magnetic fields so they’re basically like tiny bar magnets and this property is called spin. If you place them in a magnetic field they will align with magnetic field just like a compass needle lines up with the magnetic field of the earth and this is the lowest energy state so you can call it 0 state or we call it for the electron spin down. Now you can put it into one state or spin up but that takes some energy.
If we try to align this electron in other state than it naturally tends to go to, we will have to give some energy and this is the highest energy state. In principle if we were able to put it exactly against the magnetic field it would stay there. So far we are just talking about classical bit concept for electron. It has two states spin up and spin down which like the classical 1 and 0 but the interesting thing about quantum objects is that they can be in both states at once now when you measure this spin it will be either up or down but before you measure it the electron can exist in what’s called a quantum superposition and the probability of finding electron in either up or down state is determined by some coefficient. This coefficient represents the relative probability of finding the electron in one state or the other.
To realize the incredible computing power of quantum computers we need to consider an interacting quantum bits. With two electrons in discussion, there are four possible states of these two electrons. At this point you might think that its just like classical computer. With two bit information we can have four possibilities that is 00 01 10 and 11. Even though its 4 possible information, it’s just 2 bit information.
Now quantum mechanics allows us to have the superposition of these four states. So to determine the state of the qubits we need four coefficient numbers. In classical example we need only two bit information (0 and 1) to know about all four states. So in extension, if we have three qubits, it can represent eight states.
Going this way we can easily realize that N qubits can contain classical bits information. It should be noted that a quantum computer can perform more operations simultaneously; reducing the time it takes to arrive at the end result by exponentially reducing the number of computation required.