All nucleus are made up off protons and neutrons. A proton has the charge value equal to electron but the mass of electron is negligible as compared to protons and neutrons. In nuclear physics, each element is represent by {}_ZX^A where Z is the atomic number which is nothing but the number of protons and A is the mass number indicating the sum of numbers of proton and neutron and X represent the symbol of the element. Hence N (number of proton) = A – Z. The nucleus of nitrogen can be represented by {}_7N^{15} .

1. Isotopes: Isotopes are nuclei with the same atomic number but different mass number. Most of the elements have their isotopes and as an example, silicon isotopes are listed here {}_{14}Si^{28} , {}_{14}Si^{29} , {}_{14}Si^{30} and {}_{14}Si^{32} . It is to be noted that the charge present is the only thing that determines the properties of an atom. So, all the isotopes have identical chemical properties.

2. Isobars: Isobars are the nuclei with the same mass number but different atomic number. An example is {}_8O^{16} and {}_{7}N^{16} . Isobars are different elements and have totally different physical and chemical properties.

3. Isotones: Isotones are nuclei with an equal number of neutrons. Some example includes {}_{6}C^{14} , {}_{7}N^{15} and {}_{8}O^{16} .

4. Isomers: The nuclei which has same Z and A but is different in energy states and internal structure. These nuclei have different life time.

  5. Mirror nuclei: It is the nuclei having the same mass number but with protons and neutron number interchanged that is the number of proton in one is equal to number of neutrons in other. Example is {}_{4}Be^{7} and {}_{3}Li^{7}

6. Nuclear size: The size of nucleus was first roughly measured during the Rutherford’s scattering of alpha particles and the nucleus radius was estimated to be in the order of 10^{-14} to 10^{-15} meters and atomic radius in order of 10^{-10} . So, by this we can tell that atom is 1000 times bigger than its nucleus. The calculating formula for nuclear radius is

R = r_0 A^{1/3}

where R is the mass number and 1.3 \times 10^{-15}m or 1.3 fermi. By using this formula we calculate the radius of {}_6C^{12} to be 3 fermi and the radius of {}_{47}Ag^{107} is 6.2 fermi and radius of {}_{92}U^{238} is 8.1 fermi.

7. Nuclear mass: The mass of the nucleus is determined by adding up the mass of neutrons and protons in the nucleus. Thus the mass of the nucleus = Zm_p + Nm_n where m_p and m_n are mass of proton and neutron respectively. It should me noted that the mass of the nucleus is measured by mass spectrometers and the real mass of nucleus is always less than the mass calculated by formula given above. This difference is called mass defect.

8. Nuclear charge: The nuclear charge is due to proton as neutron is electrically neutral. Each proton has a charge of 1.6 \times 10^{-19} C which is also the charge of one electron.

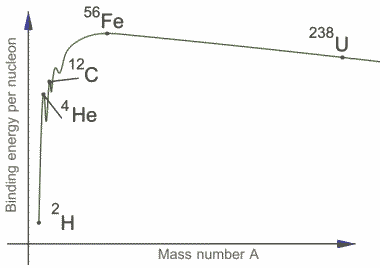
9. Binding energy: In nuclear mass we have talked about the mass defect and here is the explanation on where that mass actually goes. When Z protons and N neutrons get together to form a nucleus, some mass disappears and is converted into energy. The value of this energy is given by famous Einstein equation E = mc^2 . Here m is the disappeared mass and c is the velocity of light. This energy is called binding energy and this energy determines the stability of the nucleus. To disintegrate any nucleus, energy equivalent to or higher must be given to the nucleus. The value of binding energy is given by the formula

B.E. = (Zm_p + Nm_n - M) c^2 where M is experimentally determined mass of a nucleus.

10 Nuclear density: The nuclear density can be found out using the formula

\rho_N = \dfrac{Nuclear mass}{Nuclear volume}

Using this formula, we can find that nuclear density is 1.816 \times 10^{17} kgm^{-3} . We can see that nucleus is a very dense object and is in very compressed state.