Gauss theorem (German mathematician Carl Friedrich Gauss) is used to relate flux (the number of lines of force crossing an area normally is called electric flux or simply flux) through a closed surface to the charge enclosed by it. It states that The total electric flux through an arbitrary closed surface, enclosing the charge is equal to the ratio charge to the permittivity of the medium.

Let us consider a point charge +Q inside a closed surface and let dA be elemental area on the closed surface at a distance of r from the point charge +Q. Then the electric field intensity at the area dA is 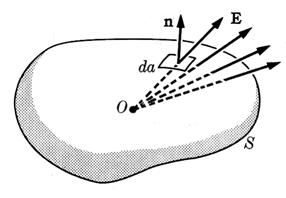gauss theorem

E = \dfrac{Q}{4\pi \epsilon r^2}

Let is assume that the direction of E subtends an angle \theta with outward normal to dA. Then the component of E normal to dA is

E_{normal} = Ecos\theta

Now the flux through dA is

d\phi =E_{normal} \times dA = E cos\theta dA

Putting the value of E

d \phi = \dfrac{Q}{4\pi\epsilon {r^2}}{dAcos\theta}

d \phi = \dfrac{Q}{4\pi\epsilon}{\dfrac{dAcos\theta}{r^2}}

The factor \dfrac{dAcos\theta}{r^2} is called solid angle subtended by dA at +Q and denoted by d\omega . Hence

d\omega = \dfrac{Q}{4\pi \epsilon} \dfrac{dAcos\theta}{r^2}

The total flux through the closed surface is obtained by integrating the equation over the complete solid angle

\int d\phi = \phi = \dfrac{Q}{4 \pi \epsilon} \int^{4\pi}_0{d\omega}

It should be noted that the minimum value of solid angle is zero and maximum value is 4\pi . So,

\phi =\dfrac{Q}{4\pi\epsilon} 4\pi = \dfrac{Q}{\epsilon}

this proves the gauss’s theorem of any arbitrary closed surface.

It should be noted that the Gauss theorem shows that the total flux crossing any closed surface drawn around a point charge is a constant and is independent of shape and size of the surface.