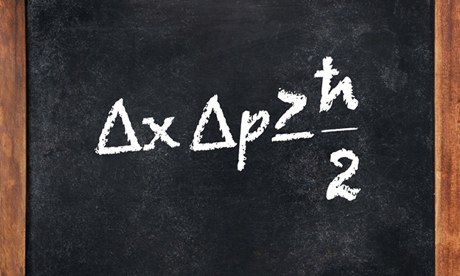The statement of Heisenberg’s uncertainty Principle is something like this “it is impossible to determine precisely and simultaneously two complementary variables to arbitrary accuracy.” These pairs of variables are called canonical conjugate and example of such variable pairs includes position and momentum, energy and time, angular momentum and angle etc. The Heisenberg’s uncertainty Principle for position and momentum is mathematically expressed as follows

\nabla q \nabla p \ge \dfrac{\hbar}{2} —- (1)

The uncertainty principle usually describe these situations

  1. It is impossible to predict states in which position and momentum are simultaneously arbitrarily well localized.
  2. It is impossible to measure position and momentum simultaneously.
  3. It is impossible to measure momentum without disturbing position and vice versa.

Hence we can say that even though a particle may contain definite momentum and coordinate, the uncertainty principle prevents us from measuring them simultaneously with considerable accuracy. Equation (1) above implies that a particle cannot simultaneously have accurate momentum and position. This inaccuracy is a natural consequence and not about imperfection of our measuring instruments.

The uncertainty principle is the manifestation of observer effect. The measurement of the position necessarily disturbs the momentum of particle.

“Physicists of today have learn that not every question about the motion of an electron or a photon can be answered but only those questions which are compatible with the uncertainty principle.” – Max Born