Blackbody radiation

A blackbody is an object that is perfect absorber of radiation. It is a material object that absorbs all radiation falling on it and hence appears black under reflection. When an object is heated, it radiates electromagnetic energy as a result of thermal agitation of electrons on its surface. The intensity of this radiation depends on its frequency and temperature. This emitted light ranges over the entire spectrum. An object in thermal equilibrium with its surrounding radiates as much as it absorbs. It thus follows that a blackbody is a perfect absorber as well as a perfect emitter of radiation.

A blackbody is constructed by taking a hollow cavity whose internal walls are constructed to be perfectly reflective of electromagnetic radiation and it has a very small hole on its surface. The radiation entering from the hole is trapped inside the cavity and gets completely absorbed after many reflections on the inner cavity wall. As absorption continues, temperature is raised and the hole will eventually begin to glow. This hole will now become perfect emitter and the radiation emitted in such condition is called blackbody radiation.

It is to be noted that the peak of the radiation spectrum occurs at a frequency that is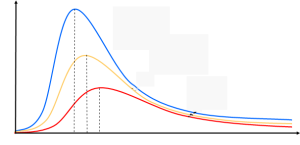 proportional to the temperature $T$ . This is the reason why a heated body emit radiation from red to yellow to white as temperature increases. This means that the peak would shift more to the right and classical theory was unable to explain the high frequency behavior of blackbody emission. To explain these results, classical theory is modified in the Rayleigh-Jeans formula. The electromagnetic energy density $u(\nu,T)$ in the frequency ranges $\nu$ to $\nu +d\nu$ is defined as:

$u(\nu,T)=N(\nu)<E>$

where $N(\nu)$ is the number of degrees of freedom for frequency $\nu$ and $<E>$ is the average energy per degree of freedom that is average energy of the oscillators present on the walls of the cavity.

According to the equipartition theorem of classical thermodynamics all oscillators in the cavity have the same mean energy, irrespective of their frequencies. Now, Rayleigh-Jeans formula is

$u(\nu,T)=\dfrac{8\pi{\nu}^2}{c^3}kT$ and this formula works well at low frequencies only.

In contrast to Rayleigh’s assumption, Plank considered that the radiation of the frequency $\nu$ can only exchange energy with matter in discrete units of energy or quanta of energy that is the energy if the radiation of frequency $\nu$ emitted by the oscillating charges must come only in integral multiples of $h\nu$ .