Photoelectric effect is one of the initial phenomena which proved the quantization of light. It was discovered by Hertz in 1887 and Thomson in 1899 confirmed that it was electron that was responsible for photoelectric effect.

Einstein was the scientist behind more detail and elaborate explanation of photoelectric effect. He postulated his theory on photoelectric effect in 1905 and said that light consist of particles called photon. Each photon has an energy of E=h\nu and the linear momentum p=\dfrac{h}{\lambda} where \nu is frequency of wave and \lambda is the wavelength of the light.

p=\dfrac{h}{\lambda} = \dfrac{h}{\dfrac{c}{\nu}} = \dfrac{h}{c(\dfrac{h}{E})} = \dfrac{E}{c}

When a beam of light of frequency \nu is incident on a metal, each photon transmits all its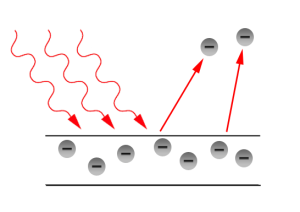Photoelectric effect energy h\nu to an electron neat the surface. In this case the photon is entirely absorbed by the electron. Thus the electron will absorb energy only in quanta of energy h\nu and intensity of incident radiation doesn’t have any effect. There is always a minimum energy which is required to knock off electron from the metal and this energy is called work function \Phi . If h\nu is larger than \Phi the electron will be knocked off and the electron will not jump if this condition is not satisfied. For h\nu > \Phi electron come out with kinetic energy with the maximum value E_e such that

h\nu = \Phi + E_e

where E_e represents the kinetic energy of the electron leaving the material. This is Einstein photoelectric equation and gives explanation to photoelectric effect and is validated by experimental observation. From this equation we can see that the ejected electron’s kinetic energy increases linearly with the incident frequency \nu .

Here E_e = h\nu - \Phi = h(\nu - \nu_0)

Here \nu_0=\dfrac{\Phi}{h} and is called threshold or cutoff frequency of the metal. This relation shows that no electrons are ejected from the metal unless \nu>\nu_0 and the frequency of radiation is important rather than the intensity of the radiation to knock off electron. The kinetic energy of the knocked off electron is acquired from the excess energy h(\nu-\nu_0) given by the incident radiation.