Binding energy is the energy that holds a nucleus together and is equal to the mass defect of the nucleus. Nuclear binding energy is the energy that would be required to disassemble the nucleus of an atom into its component parts. These component parts are neutrons and protons, which are collectively called nucleons. Let us calculate the binding energy of an \alpha particle using the concept of mass defect

Mass of 2 protons + 2 neutrons = (2\times1.007276 + 2\times1.008665)\mu

= 4.031882 \mu

Mass of \alpha particle = 4.001506 \mu

Mass defect \Delta m = (4.031882 - 4.001506) \mu = 0.030376 \mu

B.E. = (0.030376 \times 931.3) MeV = 28.29 MeV

B.E. = 45.32 \times 10^{-13} J

Binding energy per nucleon = \frac{total-BE-of-a-nucleus}{number-of-nucleons-it-contains}

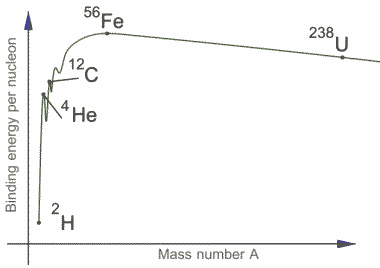
The binding energy per nucleon and the mass number is plotted in the figure. We can see that the curve rises steeply initially and then gradually reaches maximum of 8.79 MeV at A=56. This number A=56 corresponds to Iron {26}_Fe^{56} . The curve now drops very slowly to somewhere around 7.6 MeV at the highest known mass number. From this graph we can say that nuclei of intermediate mass are more stable since high amount of energy is required to separate these nucleons. This also means that a large amount of energy will be liberated if heavier nuclei can be divided into lighter ones in nuclear fission.

be-mass-number-plotPacking fraction: The ratio between mass defect and the mass number is called the packing fraction. Packing fraction means mass defect per nucleon. Packing fraction is used to measure the comparative stability of the atom.

packing fraction = \dfrac{isotopic mass-mass number}{mass number} \times 10^4

Packing fraction can be positive or negative. If packing fraction is negative, the isotopic mass is less than the mass number and in that case the mass gets transformed into energy in the formation of that nucleus according to the formula E=mc^2 . This nuclei is more stable.

A positive packing fraction would mean a tendency towards instability. This is not essentially correct for atoms will lower atomic mass though. It should be noted that the element with mass numbers more than 230 are radioactive and goes through spontaneous disintegration.

Nuclear stability

The stability of nuclei are classified according to even and odd number of protons and neutrons

Protons Neutrons Stable Nuclei
 even even 160
 even  odd  56
 odd  even  52
 odd  odd  4

For stable nuclei, we can see that nature prefers even number of protons and an even number of neutrons. The odd odd combination of proton and neutron in the nucleus are very less and are found only in lighter elements. For elements with large number of proton in the nucleus, the coulomb electrostatic force of repulsion becomes significant and the number of neutrons must be greater to compensate this repulsion effect.