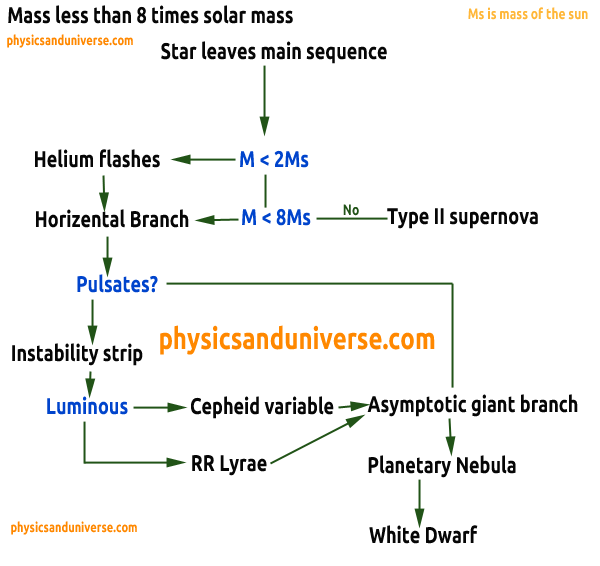
Asymptotic Giant Branch
Both hydrogen and helium burning run in the spherical shell. In this branch star has inert core of carbon and oxygen. Helium burning causes the luminosity to increase. Stars gets bigger while the temperature remains about the same. The star expands, cools but becomes more luminous. The mass of the core increases as helium burning continues in the upper spherical shell. Because of the pressure (non degenerate) exerted by the huge core mass, wind develops. Star begins to lose mass at a rate of . Last mass moves away from the star. It forms a shell around it called planetary nebula which can be easily observed in the Infrared region.
White Dwarf
A white dwarf is a small hot star of mass 1.4 times the mass of the Sun having carbon and oxygen as a central star. Stellar core more massive than 1.4 times the mass of the sun will not become white dwarfs but instead continues to shrink to become either neutron stars or black holes. White dwarf emits UV light. These energetic radiation ionizes dust and gas forming HII region called Planetary nebula as a whole.
White dwarfs are hot (~10,000 K), low luminosity stars composed mainly of carbon and Helium. Their luminosity is low because of their small surface. Electrons becomes degenerate when density becomes greater than . The electrons in white dwarfs are degenerate. The largest possible white dwarf mass is 1.4 times the mass of the sun called Chandrashekhar limit.
Since the surface area of white dwarf is small, the cooling rate is slow. The white dwarf stars does not shrink on cooling because of its electron degenerate pressure. As the star cools, its luminosity decreases. This process slows over time, so that the dimmer the stars gets, the slower it gets dimmer. No white dwarf with masses less than 0.6 times the mass of the sun have been observed. The radius of the white dwarf is inversely proportional to the cube root of its mass.